GLM.DataPrep

Reading: Goldburd, M.; Khare, A.; Tevet, D.; and Guller, D., "Generalized Linear Models for Insurance Rating,", CAS Monograph #5, 2nd ed., Chapter 4.

Synopsis: In this article you'll learn to strategize your model building by laying the groundwork for a successful build. You'll gain an appreciation of the steps involved in preparing the data so it's ready to go into a model, and understand how to effectively use your data so you can later measure model performance.

Study Tips

A lot of this is common sense but you need to be prepared to explain it quickly and concisely. Pay particular attention to splitting the data and the potential for overfitting models.

Estimated study time: 3 Hours (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• Ways to split a data set into Train/Test and why you should do this.
• How to interpret the train/test model error

Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)

reference	part (a)	part (b)	part (c)	part (d)
E (2017.Fall #4)	Train/Test Data Sets - Reasons for splitting	Model Error - Interpret Train/Test	Time Validation - describe advantage
E (2012.Fall #2)	GLM Properties - GLM.Basics	Missing Data - describe issues

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.

In Plain English!

Data preparation is an iterative process. As you clean the data you gain insight into it which helps the model building. As you build the model, you may find errors with the data which then leads to more data preparation.

The granularity of the data is important. Some rating characteristics may apply at the policy level, while others may apply at the individual risk level. An example of this is a multi-car auto policy. The age of the driver should be tied to the vehicle they drive (individual risk level), while a policy level discount should be tied to all vehicles on the policy.

A substantial challenge which may occur during the data preparation process is merging the premium/exposure data with claims data as these are typically kept on separate systems. Dealing with legacy/older systems can add to the potential issues.

Assuming there are separate claims and premium databases, what are some key questions to ask?

1. Are there timing differences between updates?
   • Such as claims updating daily but premiums/exposures at the end of each month?
2. Is there a unique key to match premiums and claims?
   • It's important to avoid double counting claims or dropping (orphaning) claims due to a lack of corresponding premium/exposure data.
   • Should ensure the correct characteristics for the claim are assigned to the vehicle/driver/coverage involved.
3. What level of data aggregation is appropriate?
   • Depends on the model and on the computing resources/time available.
   • Often aggregate to calendar:
     1. No seasonality adjustments are required
     2. Need to make sure the correct exposures are recorded: For instance, a 12-month policy written on July 1st should contribute 50% of a full exposure to that calendar year.
   • Claims data is often at the number of claims and total paid level. E.g. Two claims for $1,000 paid out in the calendar year. However, this can cause a loss of information as we don't know if it was 2x $500 or say $100 and $900. Should the data be aggregated at the claim/policy level or claimant or coverage level?
   • Should the data be geographically aggregated into territories/states/regions. This is particularly important for commercial insurance where one policy may cover multiple geographically distinct locations.
4. Are there any fields which can be discarded? Such as removing one of two highly correlated fields?
5. Are there any fields that should be in the data but aren't? For instance, credit. This may need to be obtained anonymously from a third party vendor for data protection purposes.

It usually makes sense to keep the data as granular as possible. However, recall that a GLM assumes the underlying data is fully credible...

Modifying the Data

This is also known as cleaning the data. What are some key things to check?

1. Are there any duplicate records both before and after merging?
2. Does the data present in a categorical field match the range of values in the documentation?
3. Do any continuous predictors have unreasonable values?
   • Such as negative values for age of home, exceptionally large values for age of insured (anyone aged 700?).
4. Are there any errors or missing values?

Handling Errors and Missing Values

1. Delete the records - works for known duplicate entries but can lead to loss of information. Not recommended in general.
2. Add an error flag variable and replace the value with the mean or modal (most common) value for the field. This level should be used as the base level in the model.
3. Impute the correct value by building another model on the subset of known good data with the goal of predicting the missing/erroneous value.

Other Data Modifications

1. Binning (or banding): Convert a continuous variable into a categorical variable for example by grouping driver age into Youthful, Young Adult, Adult, and Senior.
2. Reducing the number of categories by combining: For instance combining construction types Masonry and Masonry veneer into a single category called Brick.
3. Separating a field into multiple fields: For instance a two character auto liability symbol, JH, may be split into two fields called LiabSymb1 and LiabSymb2 with entries J and H respectively.
4. Combining multiple fields into one field (this is the reverse of the above example).

mini BattleQuiz 1 You must be logged in or this will not work.

Splitting the Data

This is a very important step to understand. The order in which this stage is done relative to the other steps is very subtle but can significantly influence the predictive power of your model. You should always split the data before you begin your exploratory analysis so you minimize forming assumptions about how the model should behave/what will be predictive.

The data set should be split into at least two subsets.

• Training set: This is used during all of the model building steps.
• Test/Holdout set: This is used to assess the model performance/choose the final model.

The model building process fits the best parameters to the training data set, so if we measure performance using the training data set we will get optimistic results. Further, if two models use different training data sets then it is not a fair comparison of their predictive power unless you test them on an identical data set. As the complexity of the GLM increases, the fit of the model to the training data set improves as the GLM attempts to describe all of the variation in the data. However, adding complexity may deteriorate the performance of the model on unseen data as the complexity of the model tries to capture purely random variation.

GLM model complexity is described in terms of degrees of freedom, that is, the number of parameters estimated by the model. One-dimensional continuous variables add one degree of freedom. Categorical variables add [math]n-1[/math] degrees of freedom where n is the number of levels within the category (the base level is excluded). Each additional degree of freedom gives more flexibility for the model to optimize its fit on the training data.

As the number of degrees of freedom increases, the fit of the model on the training set will always improve, until every data point is accurately predicted by the model (all variation in the training set is explained by the model). However, adding degrees of freedom and then comparing the resulting model on the test data set results in the model fit improving at first but then deteriorating as the model has been optimized to predict the training data at the expense of the underlying characteristics we want to predict. In other words, the model is picking up too much noise by trying to explain all of the random variations within the training set. Since the noise is random, it is unlikely to be the same in the test data set, so the model starts to predict poorly. The goal of the model is to explain the variation driven by systemic effects in the process (the signal) rather than all of the variation in the training data set. The model is overfit if the parameter estimates contain too much noise.

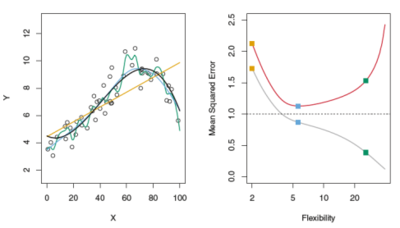
Figure 1 below is an excellent illustration of this from "An Introduction to Statistical Learning" . The black line in the left graph is a known "true" function (the signal) that is sampled with error (black circles). The sample data is split into train and test data sets then different models are fit to the training data such as a linear regression and two splines with various degrees of freedom. The graph on the right plots the mean squared error (MSE, a measure of model fit) against the model degrees of freedom (more freedom = higher flexibility) and the three models from the left graph are shown by colored squares. By comparing the test curve (in red) with the graph on the left, we see why the highest degrees of freedom model (green curve) has a low train MSE (grey curve) but a high test MSE — it fits the training data well but doesn't follow the signal well because the green curve wiggles too much as it tries to conform to the training data as closely as possible, i.e. the green model is overfit.

Figure 1

The modelling data set should be split into the training and test data sets prior to the initial exploratory variable analysis, and should be kept separate until the end of the modeling. Once modeling is complete, the test set is then used to objectively measure performance. Typically, the data is split in a 60/40 or 70/30 training/test ratio. More data in the training set will allow patterns to emerge better. However, less data in the test set means the model assessment stage is less certain.

Splitting the modelling data set into train/test can be done at random or on the basis of a time variable such as accident year. Test sets are known as out of sample if they're randomly selected, and out of time if the time periods in the train/test sets don't overlap.

Out of time validation is particularly good when modelling situations which can impact multiple records. An example of this is modelling wind claims. If the data set is split randomly then both train and test sets contain records relating to the same windstorm events. So the test data isn't truly unseen; this can give optimistic validation results. Having different time periods in the train/test sets minimizes this overlap and gives a better indication of how the model will perform in the future.

A further refinement of the train/test concept is train/validation/test. Here it's customary to split the data along 40/30/30. The model is built using the training set, and iterations of validating and then adjusting the model take place on the validation and training sets respectively. Once the modeler is happy with the product, it is tested on the test set.

A downside of using train/validation/test is the data may become too thin in each piece. Also, if the validation data set is referred to too often, then it is more like an extension of the training data set and so subject to over fitting. The same applies to referring to the test data set too often.

Cross Validation

This is an alternative to splitting the data. The most common form is k-fold validation where the data is split into k groups (usually 10) called folds. The split can be done randomly or over a time variable.

For each fold, train the model on the other [math]k-1[/math] folds and test it on the k^th fold. We get k estimates of the model performance, each of which was assessed on data that hadn't been seen during the modelling process. Comparisons between several models can be made by comparing the relative performance for each fold.

For effective cross validation, it must encompass all of the model building steps. This limits its application to GLMs for insurance purposes because a lot of work in this situation is selecting the variables and transforming them. This work would need to be repeated k-times which would be costly and time consuming. If all of the data was used to evaluate which variables to include or exclude, then the holdout fold isn't truly unseen data.

Cross validation is appropriate when there is an automated variable selection process. The same selection process can be run on each fold and then cross validation would yield the best estimate for out of sample performance.

One area within insurance modelling where cross validation may be used is within the training data set to tune the parameters of a variable. For instance, when fitting a polynomial, k-folds could be used to determine the best linear fit. The same k-folds are then used for the best quadratic fit. The comparison between quadratic and linear fits then takes place within folds before making a decision on the final fit which is then run with all of the training data to generate the best coefficients.

mini BattleQuiz 2 You must be logged in or this will not work.

Modelling Strategy

The following levels of modelling complexity increase in terms of the time and effort required.

1. Keep the current model.
2. Keep the current model and update the coefficients (factors).
3. Add new variables to the current model and calculate new coefficients.
4. Add interaction terms, sub-divide categorical variables,...

Build each level of model using the same train data set (and same validation data set if available). Once all models are complete, measure each model on the test data set to compare their relative performance. Combine this with business insight to select the final model.

Once the final model is chosen, re-run it using all of the available data (train/(validation)/test) to produce the most accurate estimate of the coefficients.

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.