Holmes.Transformations

Reading: Holmes, T. & Casotto, M, “Penalized Regression and Lasso Credibility,” CAS Monograph #13, November 2024. Chapter 3 Sections 3.4 – 3.5.

Synopsis: This is a brief reading which covers how to code various types of data for inclusion in the penalized GLM framework. We explore the impact of penalization on the coefficients for each different type of variable.

Study Tips

Read this material fairly quickly and do the flashcards from time to time. There are other places in the syllabus that you should focus more on rather than spending lots of time here.

Estimated study time: 1 Hour (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• How the base level affects model output for GLMs and penalized regression.
• How to interpret model output for continuous variables.
• How to use lasso regression for variable selection.
• Describe the ways of incorporating control variables into lasso regression.

Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)

reference	part (a)	part (b)	part (c)	part (d)
Currently no prior exam questions

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.

In Plain English!

In this reading we look at how to transform variables for use in lasso regression and the impact that the penalty has on these transformations.

Categorical Variables

A categorical variable takes a value (level) from a discrete list of possible choices. One level is chosen to be the base level — we usually choose the level with the greatest exposure volume. The remaining non-base-level values are modeled independently in the design matrix, resulting in each non-base-level having its own [math]\beta_j[/math] coefficient. This is known as one-hot encoding. When a level is deemed insignificant, the coefficient is set equal to zero to remove the level from the model. The removed level should be grouped with the base level and the model refitted. This approach holds whether using a penalized or unpenalized GLM.

Lasso regression with a sufficiently large penalty parameter will set some coefficients to zero automatically. This indicates a natural grouping of less significant levels with the base level. For material levels, lasso regression provides the credibility weighted deviation from the base level.

Question: Briefly describe how the model output changes when a different base level is selected when using a/an:       a.) Unpenalized GLM       b.) Penalized Regression (GLM)

Solution:

• When using an unpenalized GLM, changing the base level of a variable does not alter the beta coefficients. It does affect the confidence intervals and p-values though.
• However, when using penalized regression, the beta coefficients will change if a different base level is used.

Continuous Variables

Categorical variables identify a change in level and continuous variables identify a change in slope.

The simplest continuous variable is a linear representation which has a single [math]\beta[/math] coefficient in the (penalized or unpenalized) GLM framework. This coefficient represents the slope of the impact. Lasso regression shrinks or sets this coefficient to zero. Assuming a log-link function, a positive beta coefficient that is shrunk under lasso regression results in a reduction in the slope. Whereas if the beta coefficient is negative, shrinking it towards zero results in an increase in the slope.

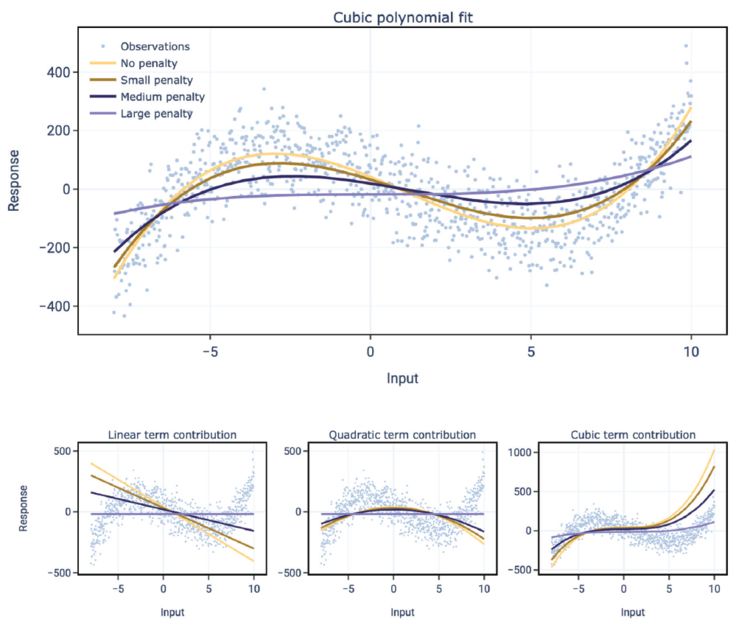
More complex, non-linear representations may be captured by introducing additional beta coefficients. For example, a third-degree polynomial may be modeled via [math]\beta_1x+\beta_2x^2+\beta_3x^3[/math]. Lasso regression will individually shrink each of these beta coefficients but looking at the individual coefficients is not particularly helpful. Instead we should look at the linear combination to determine the overall effect.

Figure 3.11

Figure 3.11 above is taken directly from the source material. It illustrates how looking at impact of lasso regression on the individual coefficients is less insightful than looking at the impact across the polynomial at once.

Question: Identify a drawback of using lasso regression to select polynomial coefficients.

Solution:The coefficients, [math]x, x^2, x^3[/math], etc. are highly correlated predictors in the model. Lasso regression produces suboptimal results in the presence of highly correlated predictors because different terms will be excluded from the model at different times depending on the selected penalty parameter.

Holmes and Casotto go on to state: "Using lasso to determine the optimal combination of feature transformation is not recommended."

Feature engineering/feature transformation using polynomials, linear or cubic splines, etc. is better performed via elastic net regression.

Ordinal Variables

An ordinal variable is a categorical variable with an ordering assigned to the levels. For example, a "Highest Education" variable may consist of "High School", "Some College", "Bachelor's degree", "Master's", or "PhD" — there is an implicit ordering here that Bachelor's is better than Some College, Master's is better than Bachelor's etc.

In contrast, a nominal variable is a categorical variable with no order/relationship between the categories. For example, an "Eye Color" variable may consist of "Blue", "Brown", "Green" and "Grey" and there's no implicit reason to say this ordering is any better than say "Green", "Grey", "Blue", and "Brown".

Treating a variable as ordinal means usually means encoding the variable using integers: 0 for High School, 1 for Some College, 2 for Bachelor's and so on. Holmes and Casotto say that "an ordinal treatment of a variable relies not on the numeric values of the variable but instead on stepwise indicators". However, they do not demonstrate what this means. They do allude to an iterative nature as "when a coefficient is zero, it results in the grouping of two consecutive levels.

This brings us to a key advantage of the lasso penalty. It allows us to model nonlinearity in a more efficient way than an unpenalized GLM.

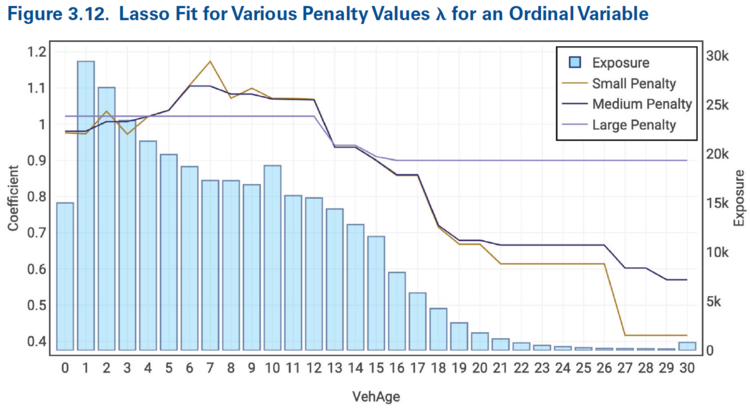
Figure 3.12 below demonstrates this. We see that as the size of the penalty increases we get (more and/or larger) horizontal segments appearing in the vehicle age coefficients. A horizontal segment says neighboring vehicle ages have the same coefficient, i.e. the lasso regression has automatically grouped them together.

Figure 3.12

Another advantage of using ordinal variables is they can help choose an actuarially sound penalty parameter. In Figure 3.12 above we see the "small" penalty results in some illogical rating where VehAge 7 has a larger coefficient than neighboring ages 6 and 8. Increasing the penalty parameter to "medium" automatically smooths out this reversal. In general, we can start with the "optimal" penalty parameter and then increase it gradually until any unintuitive behaviors have been penalized out of the model.

Control Variables

A control variable is used in a model to prevent signal flowing into other characteristics. For example, when modeling pure premiums using data that has not been developed to ultimate, including an accident year control variable in the model will capture signal which reflects older losses are more developed than more recent losses. The rest of the model then focuses on measuring the differences due to the risk characteristics.

In an unpenalized GLM the control variables are left in the model regardless of whether they are statistically significant. With lasso regression, some of the control variable levels may be removed from the model by the penalization.

Question: Briefly describe two reasons why it's okay to allow control variables to be fitted and penalized along side other variables in a model.

Solution:

• Fitting control variables at the same time as other variables allows the model to allocate signal appropriately between the control variables and any other model variables which may be correlated with the control variables.
• If a control variable (or level within) is removed from a model via penalization it's unlikely that the limited signal would have had a material effect on any correlated predictors.

A stepwise approach can be used if the modeler wants the control variable to have as much signal as possible. First the control variables and, optionally, a few critical predictors, are fitted using a model with no or a small penalty parameter. The resulting coefficients are then offset in a secondary model which uses an appropriately sized penalty term. Since offsets are fixed coefficients, they are not subject to penalization (they would alter the penalty term by a constant amount).

Lasso for Variable Selection

Using lasso regression for variable selection means starting with a penalty parameter which is large enough to remove all variables from the model. The penalty parameter is then gradually decreased until variables enter the model. This is not possible with ridge regression because the coefficients are never directly set equal to zero.

CAUTION! This approach produces suboptimal results when there are highly correlated predictors because not all correlated predictors enter the model at the same time. Actuarial judgment should be used to select between highly correlated predictors (e.g. when fitting polynomials etc.) before using lasso regression for variable selection.

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.