Holmes.LassoCredibility

Reading: Holmes, T. & Casotto, M, “Penalized Regression and Lasso Credibility,” CAS Monograph #13, November 2024. Chapter 5.

Synopsis: In this reading we introduce the lasso credibility technique which is Holmes and Casotto's key contribution to the field of actuarial science in this monograph. We explore how restricting to ordinal and categorical variables allows us to introduce actuarially appropriate complements of credibility via offset terms in the lasso regression framework. We examine the practical implications associated with choosing a suitable penalty parameter and conclude with a discussion on translating the output of the lasso credibility technique into a rating plan.

Study Tips

• This is a fairly quick read which introduces a central concept to the monograph. There is scope for some relatively easy calculation questions but, in our opinion, most of the exam questions would likely be short-answer focused on the theory.

Estimated study time: 2 Hours (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• How to choose and use actuarially appropriate offsets to form the lasso credibility technique.
• How to choose a suitable penalty parameter.
• How to translate the output of a lasso credibility model into rating factors.

Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)

reference	part (a)	part (b)	part (c)	part (d)
Currently no prior exam questions

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.

In Plain English!

So far our penalized regression approach has used [math]\beta = 0[/math] as the complement of credibility. However, this may not always be appropriate so we look to enhance the process.

Three things are required:

• All variables must be categorical or ordinal.
• For each variable, we must specify an offset which represents the complement of credibility.
• Penalized regression is used as the credibility procedure.

While the approach can be done using ridge or elastic net regression, Holmes and Casotto say it's best applied using lasso penalization. From now on, we'll refer to this approach as lasso credibility.

By preventing the model from using continuous variables, we are using variables whose coefficients will represent the magnitude of change between categories within each variable. Continuous variables such as Age should be treated as stepwise ordinal variables, i.e. broken into discrete groups with a natural order. The groups should be sufficiently granular to let the lasso credibility model perform grouping rather than assuming an existing level of grouping. In practice this means something like bucketing an Age variable into single years even though we may view some of these buckets to have little to no credibility. The lasso credibility approach will automatically remove steps with no credible differences while including those that have a credible difference. This allows us to fit complex and unknown deviations from our chosen complement of credibility with ease.

In a traditional GLM an offset is added to all records in the data set without a corresponding predictor variable. It is a column of fixed coefficients as the offset may vary between the records. For example, a loss elimination ratio analysis may have been completed in an external analysis to price deductibles. The deductibles are offset in the GLM. Each record gets an offset which is the transformed (matches the scale of the link function) deductible factor.

In general, for a traditional GLM, we have:

[math]g(\mu_i) = \beta_0 + \beta_1 \cdot X_{i,1} + \ldots + \beta_p \cdot X_{i,p} + \textrm{Offset}_i [/math]

Since a GLM assumes the underlying data is fully credible, we get the same model predictions whether or not we include an offset term. The model coefficients will vary but not the model predictions.

We now abandon the idea of an offset being something which accounts for an external influence like a limit or deductible. We use the concept of an offset to decompose each traditional coefficient into a linear combination of an offset coefficient and a variable coefficient.

[math] g(\mu_i) = \beta_0 + (\beta_{1,\textrm{Offset}_i} +\beta_1)\cdot X_{i,1} + (\beta_{2,\textrm{Offset}_i}+\beta_2)\cdot X_{i,2} + \ldots + (\beta_{p,\textrm{Offset}_i}+\beta_p)\cdot X_{i,p} [/math]

Each [math]\beta_{j,\textrm{Offset}}[/math] is fully determined by the modeler and are known as fixed components. The [math]\beta_j[/math] are known as variable components and are determined by the data and modeling methodology.

If there is no offset then a traditional GLM will output [math]\beta_{j,\textrm{GLM}}[/math] coefficients while if there is an offset present, a traditional GLM will output [math]\beta_j[/math] coefficients such that [math]\beta_{j,\textrm{Offset}} + \beta_j = \beta_{j,\textrm{GLM}}[/math].

To apply lasso credibility we must include an offset term for each rating variable level.

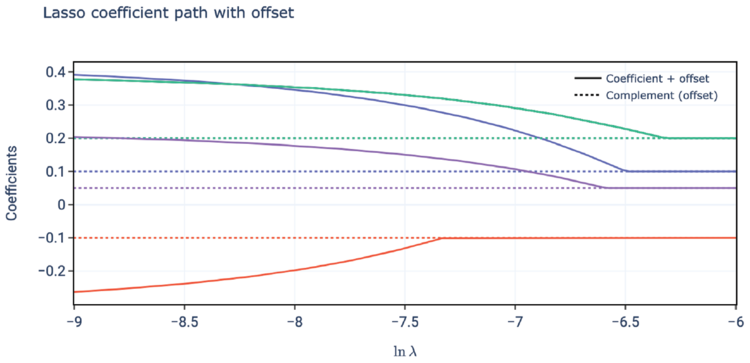
When we apply lasso credibility, as the size of the penalty parameter, [math]\lambda[/math], increases we draw the [math]\beta_j[/math] coefficients closer to zero. In turn, this means the model coefficients approach the offset coefficients, [math]\beta_{j,\textrm{Offset}}[/math]. Conversely, as the penalty parameter approaches zero then the model coefficients converge on the traditional GLM coefficients.

Mathematically,

[math]\textrm{Coefficient}_j = (\beta_{j,\textrm{Offset}} + \beta_j) = Z_j\cdot \beta_{j,\textrm{GLM}} + (1-Z_j)\cdot \beta_{j,\textrm{Offset}}[/math]

All this demonstrates the lasso credibility approach behaves like a credibility procedure. It is perhaps best seen by looking at an example of the coefficient paths in this situation.

Figure 5.1

mini BattleQuiz 1 You must be logged in or this will not work.

Alice: "So what options do we have for choosing all these complements of credibility?"

When choosing the complements of credibility for use in a lasso credibility approach you must follow Actuarial Standard of Practice No. 25. Holmes and Casotto list the following as potential options for a pure premium loss model:

• A 1.000 relativity
• A prior loss model's relativities (factors)
• A countrywide loss model that includes the data being modeled as a subset
• An existing rating plan
• Competitor relativities (factors)
• Industry relativities (factors).

Alice: "The source doesn't explicitly say this but you must match the scale of the link ratio. For example, if using a log-link then a complement of a 1.000 relativity corresponds to an offset coefficient of 0 because 1.000 = e⁰."

The default offset assumption is the offset coefficients are zero. When all offset coefficients are zero we are performing lasso regression rather than lasso credibility. When performing lasso credibility we should use the default offset assumption when we have no prior knowledge of a variable's effect on risk, and include an appropriate complement when we have suitable knowledge.

Selecting and Evaluating a Penalty Parameter for Lasso Credibility

It's still appropriate to use k-fold cross validation to guide our selection of the penalty parameter, [math]\lambda[/math]. This approach will produce an optimal penalty parameter in a statistically sound manner. However, the actuary/modeler may wish to deviate from this, particularly if there is material variation in the optimal penalty parameter across folds.

Question: Describe four scenarios where it is appropriate to judgmentally increase the penalty parameter beyond its statistically indicated optimal value.

Solution:

• Mitigate Policyholder Impacts: If the complement of credibility is derived from the current rating relativities then increasing the penalty parameter produces model output which lies between the current and optimal indicated output. This reduces the impact to policyholders.
• Factor Instability: If certain variables show instability in their relativities across the folds then increasing the penalty parameter provides additional stability through smoothing ordinal variable curves for example.
• Volatility: Your modeling data may have been adjusted for trend, developed to include Incurred But Not Reported (IBNR) claims, or have case reserves which are based on generic estimates (e.g. all Collision claims have their reserve first set at $1,000 irrespective of the actual damage). These adjustments can dampen volatility, making the data seem more credible than it actually is. Increasing the penalty parameter reduces the credibility we assign to the data, which can then introduce some volatility.
• Experience: In a bit of a circular argument, Holmes & Casotto say increasing the penalty parameter is permissible if the modeler believes the selection produces a more actuarially sound model given all of the available information.

Question: Briefly explain why selecting a penalty parameter which is higher than the optimal penalty parameter is considered generally to be actuarial best practice.

Solution: Selecting a higher estimate for the penalty parameter is more conservative and is similar to the concept of selecting a value "between current and indicated" when using traditional actuarial analyses.

Question: Briefly describe three scenarios where it may be appropriate to choose a lower than optimal penalty parameter.

Solution:

• Deficiencies: If you're pricing a line of business where the complement is known to have some deficiencies then using a lower than optimal penalty parameter pulls you further away from the potentially erroneous complement.
• Magnitude: If the modeler knows there has been change of significant magnitude from the selected complement of credibility (causing the complement to be less relevant) then decreasing the penalty parameter is appropriate to place less weight on the complement.
• Outdated Experience: If the relevant experience (the complement) is from an older or more out of date source then choosing a lower than optimal penalty parameter will give greater weight to the more recent subject experience (the modeling data set).

Calculating Indicated Rates in Lasso Credibility

Let's look at how we come up with tables of rating factors when using lasso credibility. Recall the general GLM framework is given by:

[math]\begin{array}{ll}g(\mu_i) &=& \beta_0 + \beta_1\cdot X_{i,1} + \beta_2\cdot X_{i,2} + \ldots + \beta_p\cdot X_{i,n}+\textrm{Offset}_i\\ &=& \beta_0 + (\beta_{1,\textrm{Offset}} + \beta_1)X_{i,1} + (\beta_{2,\textrm{Offset}} + \beta_2)X_{i,2} + \ldots + (\beta_{p,\textrm{Offset}} + \beta_p)X_{i,p}\end{array}[/math]

The [math]\beta_j[/math] coefficients are the model output and these must be added onto the offset coefficients to produce the final predictions once the link function is inverted.

If the model penalized out say [math]\beta_1[/math] then the model gives full credibility to the offset term [math]\beta_{1,\textrm{Offset}}[/math]. If we were using the prior rating plan factor as the offset for the variable then the model produces identical output in this situation.

When a log-link function is used the indicated model coefficients are easily turned into relativities (factors) by exponentiation. Returning to the general GLM framework we may write:

[math]\begin{array}{ll}g(\mu_i) &=& \beta_0 + (\beta_{1,\textrm{Offset}} + \beta_1)X_{i,1} + (\beta_{2,\textrm{Offset}} + \beta_2)X_{i,2} + \ldots + (\beta_{p,\textrm{Offset}} + \beta_p)X_{i,p} \\ \mu_i &=& e^{\beta_0 + (\beta_{1,\textrm{Offset}} + \beta_1)X_{i,1} + (\beta_{2,\textrm{Offset}} + \beta_2)X_{i,2} + \ldots + (\beta_{p,\textrm{Offset}} + \beta_p)X_{i,p}} \\ &=& {\color{red}e^{\beta_0}}\cdot {\color{blue}e^{\beta_{1,\textrm{Offset}} X_{i,1}}} \cdot {\color{green}e^{\beta_1 X_{i,1}}} \cdot\ldots\cdot e^{\beta_{p,\textrm{Offset}} X_{i,p}}e^{\beta_p x_{i,p}} \\ &=& {\color{red}\textrm{Intercept}} \cdot \left({\color{blue}\mbox{Var. 1 Offset}} \cdot {\color{green}\mbox{Var. 1 Relativity}}\right) \cdot \ldots \cdot \left(\mbox{Var. p Offset} \cdot \mbox{Var. p Relativity}\right) \\ &=& {\color{red}\textrm{Intercept}}\cdot\left({\color{purple}\mbox{Var. 1 Factor}}\right)\cdot\ldots\cdot\left(\mbox{Var. p Factor}\right) \end{array}[/math]

Alice: "Let's be abundantly clear about some terminology as Holmes and Casotto play a bit loose with it at times. A model coefficient is the direct output of the model prior to inverting the link function. A (model) relativity is the result of applying the inverse of the link function to the model coefficient. An offset relativity (my terminology) is the result of applying the inverse of the link function to the offset used in the model. Lastly, a factor is the combination of the offset relativity and the (model) relativity. When we have a log link function the factor is the product of the offset relativity and the (model) relativity.

In the situation where there are no offsets then the model relativities and factors are identical."

Question: Identify an advantage of lasso credibility over a GLM or lasso penalized regression model.

Solution: According to Holmes and Casotto, an advantage of lasso credibility is it allows us to use data sets which are too small to build either a GLM or a lasso penalized regression model.

Question: Briefly explain why the lasso credibility technique enhances penalized regression.

Solution: By incorporating a complement of credibility via offset terms, the lasso credibility technique reflects credible signal (where available) and shrinks volatile experience toward an appropriate complement.

A GLM may be unstable due to correlated predictors and limited data (remember GLM's assume the underlying data is 100% credible). Lasso penalized regression may shrink too many variables to zero. Lasso credibility enhances lasso penalized regression by channeling the shrinkage towards an actuarially appropriate complement.

mini BattleQuiz 2

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.