Holmes.BiasAndVariance

Reading: Holmes, T. & Casotto, M, “Penalized Regression and Lasso Credibility,” CAS Monograph #13, November 2024. Chapter 4.

Synopsis: In this article we examine the bias-variance trade-off and how this problem is approached in a traditional GLM. We see how penalized regression improves on the traditional GLM approach and explore how it can be viewed as a form of credibility weighting.

Study Tips

This article is heavy on theory and lays the groundwork for the next chapter so you'll probably want to read it a couple of times. There probably isn't a lot of calculation type problems that could be asked; instead expect short answer or the new multiple choice or mix and match type of problems to arise.

Estimated study time: 4 Hours (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• Careful selection of the penalty parameter allows us to find the optimal bias-variance trade-off
• The penalty parameter adjusts the coefficients based on both the volatility and credibility of the underlying data.
• The significance threshold is statistically determined instead of relying on the modeler's judgment and choice of p-values.

Questions from the Fall 2019 exam are held out for practice purposes. (They are included in the CAS practice exam.)

reference	part (a)	part (b)	part (c)	part (d)
Currently no prior exam questions

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.

In Plain English!

In Figure 3.8 we saw how the performance of a penalized GLM model improved as the penalty parameter, [math]\lambda[/math], increased up to a point before its performance deteriorated. Since [math]\lambda \geq 0[/math] and [math]\lambda=0[/math] corresponds to a traditional unpenalized GLM, this means a properly tuned penalized GLM will outperform a standard unpenalized GLM. This is due to the bias-variance trade-off.

Alice: "It's important to remember that in machine learning/data science, "bias" does not refer to a protected class of observations (such as race or gender)."

Bias represents the error between the model being built and the "real/true" model. Bias is a measure of how well our model captures the complexities of the problem being modeled. A model with high bias does not produce particularly useful output and is often described as underfit. Increasing the volume of data won't address the problem that our predictors simply aren't very useful!

Variance represents the model error that comes from using our modeling data set rather than a different one which is larger and richer in features/information. A model with high variance is often described as overfit since it does not generalize well because the coefficients have significant uncertainty.

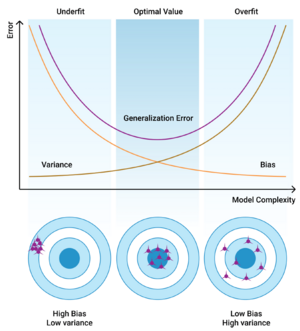
Holmes & Casotto include the following illustration which nicely outlines the concepts of bias and variance.

Figure 4.1

In Figure 4.1 above we see that a model with high bias and low variance is one that produces consistent output that is off-target. The model is not capturing enough signal to make accurate predictions. Increasing the volume of data would improve the accuracy a little bit but we'd need a richer dataset with more features (potential predictors) to really improve the accuracy as the model is too stable/simplistic.

We also see that a model with low bias and high variance is one that is on-target but with a wide range of variation in output. We can reduce the variance in our models by increasing the volume of data as this would improve the accuracy of our estimated coefficients.

Figure 4.1 motivates the following equation:

Mean Squared Error = Bias² + Variance

The goal of modeling is to reduce the mean squared error (which Holmes and Casotto refer to as the generalization error). Unfortunately, reducing the bias invariably increases the variance and vice versa so minimizing the mean squared error requires finding the optimal bias-variance trade-off.

When modeling using a standard unpenalized GLM we may decide some model coefficients are not statistically significant and remove those coefficients from the model by setting them equal to zero. We may even remove certain variables entirely. This is introducing bias which is the difference between what the true coefficients should be and zero which is what we chose them to be. Any two observations whose characteristics are identical except for some level/variable we removed will have the same model output, generating the same contribution to the mean squared error. By setting coefficients equal to zero we may be moving our model too far away from the "real" model.

In contrast, had we left the coefficients in the model then those same two observations would now have different predictions (model output) and the variance increases.

Including too many variables and levels in our model increases the variance and likelihood of overfitting. Removing too many variables/levels makes our model unrealistically stable and likely to be under fitted as we may be excluding relevant information.

mini BattleQuiz 1 You must be logged in or this will not work.

Evaluating the Bias-Variance Trade-Off

Two traditional measures of the bias-variance trade-off are:

Akaike Information Criterion (AIC) = 2NLL(β) + 2 * [# degrees of freedom]

Bayesian Information Criterion (BIC) = 2NLL(β) + log(n_obs) * [# degrees of freedom].

These are penalized measures of fit because they represent both the quality of the fit (via the Negative Log-Likelihood term) and the model complexity (via the degrees of freedom).

The bias-variance trade-off asks if increasing the model complexity produces a larger decrease in the NLL than the corresponding increase in the degrees of freedom.

Holmes & Casotto illustrate this using the following simple Homeowners GLMs. Their first model includes two predictors: Age of Home and No Fire Extinguisher. Their second model only includes the Age of Home variable. For two risks whose only difference is that one has a fire extinguisher and the other doesn't, the first model produces two difference outputs while the second produces the same output for both risks. So the first model has greater variance than the second.

If the AIC (BIC) is lower for the first model than the second then we prefer model 1. We would say model 2 is underfit and biased because it has removed a variable (No Fire Extinguisher) compared to model 1.

Conversely, if the AIC (BIC) is lower for the second model than the first then we prefer model 2. We would say model 1 is overfit and has too much variance because adding a variable (No Fire Extinguisher) didn't materially improve the fit relative to the complexity it added to the model.

The only tools available when building a traditional GLM is the addition or removal of variables. This means we cannot simultaneously improve both the bias and variance as we must perform a post-hoc analysis (using AIC or BIC for example) to determine whether our proposed model is an improvement. In contrast, a penalized GLM automatically incorporates this post-hoc analysis into the fitting procedure.

There is a distinct similarity between AIC and penalized regression. AIC looks very much like NLL(β) + λPenalty(β). It seems reasonable to ask if we could use a version of AIC in a penalized regression process. If we define the penalty term as the number of degrees of freedom (# non-zero β coefficients) then this is known as the best subset selection problem. The idea is we would compute the best GLM given a constraint on the complexity of the model. The only trouble is this problem is numerically intractable in that it cannot be resolved in a reasonable amount of time. It turns out that the best numerically tractable approximation to the best subset selection problem is lasso regression!

Alice: "Holmes and Casotto also remark that under certain conditions lasso regression will outperform best subset selection and those conditions happen to often be present in insurance data."

The Bias-Variance Trade-Off and Credibility

A traditional GLM or univariate analysis may indicate a relativity of say 1.200. However, the modeler knows the data is thin/not particularly credible so decides on an a priori basis that in the absence of other information the true relativity is 1.100. The introduction of an estimate based on something other than our data introduces bias to our model.

The credibility-weighted relativity is then 1.200 * Z + 1.100 * (1 - Z). The credibility, Z is calculated to maximize the bias-variance trade-off. It reduces the variance of the estimates through the careful introduction of an informed bias in the form of the chosen complement.

We can view the shrinkage introduced by penalized regression in a similar way. Penalized regression introduces a bias through the penalty which reduces the variance by preventing the coefficients from moving too far away from zero. The advantage of penalized regression is the optimal bias is calculated during the fitting process rather than via an iterative process of model fitting followed by post-hoc model goodness-of-fit evaluation.

Penalized Regression and Credibility

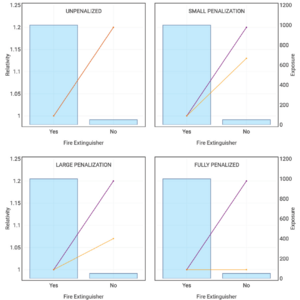
Figure 4.2 below is taken directly from the source. It shows how their simple Homeowners GLM which contains two variables, Age Of Home, and No Fire Extinguisher, responds to having a lasso penalty term included. The purple lines show the indicated result from a univariate/the unpenalized GLM, while the orange lines show the output of the lasso regression. The blue bars show the exposure for each level using the secondary axis. Note that these graphs show the relativity, i.e. we have inverted the log-link function assumed in this model.

Various sizes of penalty parameter are considered with the top left showing the unpenalized GLM ([math]\lambda = 0[/math]) through to the bottom right which shows the fully penalized GLM. By fully penalized we mean the penalty parameter is larger than the threshold which forces the No Fire Extinguisher coefficient to be zero.

Figure 4.2

We can view this as a credibility weighting where the coefficient, β_i, is a weighted average of the GLM indication and 0

[math]\beta_i =\beta_{GLM}\cdot Z + 0\cdot (1-Z)[/math]

Alice: "Something to remember — we can't calculate Z directly from the selected penalty parameter. It will vary depending on which variable we're investigating."

Conclusions

General Key Takeaways Penalized regression applies a penalty term which restricts the size of the coefficients when we perform a maximization of the likelihood (or a minimization of the negative log-likelihood). Carefully selecting the penalty parameter allows us to find the optimal bias-variance trade-off which minimizes the generalization error. This removes the need to perform post-hoc significance testing on the coefficients and subsequent iterations of modeling. The penalty parameter, [math]\lambda[/math], adjusts the coefficients based on both the volatility of the underlying data and its credibility. Variables which are not fully credible have their coefficients shrunk towards zero during the fitting process and are completely removed if they have zero credibility.

Lasso Penalization Takeaways Allow us to answer "Is this coefficient credibly not zero and how much can we trust it? As opposed to: Is this coefficient likely not zero or more extreme? Provides a statistically based estimate of how much a coefficient can be trusted rather than a post-hoc judgment based decision to include or exclude a variable in a GLM. Optimizes the bias-variance trade-off during the model fitting process rather than relying on sufficient post-hoc analysis to determine a set of variables which produce what one hopes is close to the optimal set of coefficients. The optimization occurs in a multi-variate setting so correlations are taken into account. Whereas in an unpenalized GLM, decisions are made on a variable by variable basis (typically using p-values). The significance threshold is determined by finding the optimal penalty parameter via statistical means rather than through a judgment call of say p-values over 0.05 are insignificant. Noncredible variables are automatically removed during the fitting process.

mini BattleQuiz 2 You must be logged in or this will not work.

Full BattleQuiz

Excel Files

Forum

You must be logged in or this will not work.