W-Clark-ProperPerRisk3
I didn't follow the method to determine the exposure factor (in column O of that spreadsheet). These quite a bit of excel magic going on here between the nested if, the indexmatch, and the linest formula. Can you explain in words.
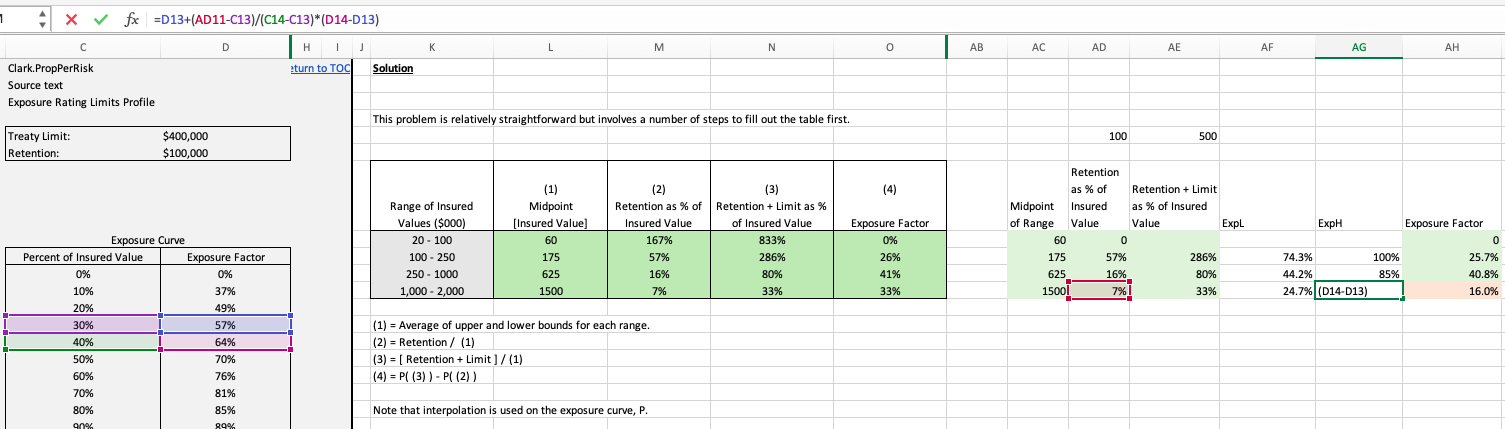
I didn't get the right answer for the highest range
ExpL = =D10+(AE28-C10)/(C11-C10)*(D11-D10) = .247
ExplH = =D13+(AE28-C13)/(C14-C13)*(D14-D13) = .4067
ExpFactor = ExpH - ExpL = 16%. Howver the solution shows 33% for this range.
Also on the exam - do you think we need to explain the method? Will all of those formulas be available in the pearson environment?
Comments
Yes, in the exam you'll definitely need to clearly explain your work/how you applied the method. The new post-exam summary from the CAS said last time there were considerable points docked for unclear calculations :(
We have reviewed the Pearson list of spreadsheet functions and restricted ourselves to ones that are in the environment.
That said, our calculation is perhaps unnecessarily complex. In the exam you just need to clearly demonstrate where your figures come from - so you wouldn't have to worry about using an index-match perhaps. However, using an index-match does ensure you don't look up the wrong figure by accident in the heat of the exam - but does assume you can type the formula correctly under pressure - swings and roundabouts...
Here's an overview of what our solution is doing.
Cols L, M and N are self-explanatory
Columns P - U are associated with Column M which deals with the retention as a % of the insured value.
Column P looks up the closest exposure factor in the exposure curve which is smaller than the column M value. Column Q looks up the closest exposure factor in the exposure curve which is larger than the Column M value. These are the y-values we need to interpolate between.
Columns R and S use the exposure curve to find the associated x-values for the figures in cols P and Q.
Columns T and U are an array formula (which works in the Pearson environment and can be really helpful). This gives the intercept and coefficient of a linear interpolation between the y values in cols P and Q and the x values in cols R and S.
Columns V through AA repeat this idea but applying it to the column N (retention + limit as a percent of the insured value).
The exposure factor in column O applies the respective linear interpolation to each of the values in columns M and N and takes the difference between them. The IF statement is used to cap values in columns M and N at 120% first so we don't exceed the exposure curve domain and extrapolate too far.
At a quick glance, your last calculation is not interpolating correctly for the retention (7%) value.
Got it thanks. Yep messed up my interpolation as I tried to "borrow" from what I had done on the prior row - and messed up the the excel.
Appreciate the detail answer - as well as the point that CAS does dock points for unclear formulas. Does that happen even if answer is correct - or just when they are trying to determine partial credit.
I would have thought that actuarial graders would love trying to trace all of these excel formulas :)
Unfortunately the CAS exam process is pretty opaque so we don't have great insight into how they assign points. Speaking as someone who has spent a fair amount of time teaching in the US university system, graders tend to be under tight deadlines with a lot of papers to cover. So if you have the right answer and the broad pieces/steps are all there then it may be easier to give most of the credit than it is when you have to painstakingly piece together each step to see if it goes anywhere close to the right direction. I imagine the CAS graders are somewhat similar but that's speculation on my part.