Bahnemann Problem 5.1
The problem says:
"The claim-size random variable X for a claim process has an exponential distribution with mean 1000. The expected number of claims for the ground-up process is 20. However, policy conditions limit claims to the layer between 1000 and 3000."
Part (a) wants us to find the mean and variance of the layer claim size.
My first issue is the statement of the question. The wording "policy conditions limit claims to the layer between 1000 and 3000" is unclear to me, and there are a few scenarios it could be:
1) Claims are reduced by 1000 (the "usual way"): so we pay 0 on claims in (0, 1000), X-1000 on claims in (1000, 4000], and 3000 on claims over 4000
2) Claims are not reduced by 1000 (how it reads to me): so we pay 0 on claims in (0, 1000), X on claims in (1000, 3000] and 3000 on claims over 3000
First all assume we're in Scenario 1: This seems like it should be a straight-forward application of formulas (5.11) and (2.2):
Then E[X; a+L] = E[x; 1000+3000] = (1/1000)*integral(x*e^(-x/1000)dx, 0 to 4000) + 4000(1-F(4000)) = 908.42 + 73.26 = 984.68
E[X;a] = E[X; 1000] = (1/1000)*integral(x*e^(-x/1000)dx, 0 to 1000) + 1000(1-F(1000)) = 264.24+367.88 = 632.12
1-F(1000) = e^(-1) = .3679
Putting it all together, (984.68 - 632.12)/(.3679) = 958.30
So now assume we're in Scenario 2, here we can't use the E[X;a]- type formulas, but I think it's still do-able. The expected claim size in 1000 to 3000 should be:
integral(x/1000*e^(-x/1000)dx, 1000 to 3000)/(F(3000)-F(1000)) = (536.61)/(.9502-.6321) = 1686.92
Then we have the portion above 3000: 3000(1-F(3000)) = 149.36
Putting these together gets 1836.28.
So neither of my answers are close to the value the book gives as 865 and I'm not sure if I'm reading the problem wrong or doing the math wrong or what.
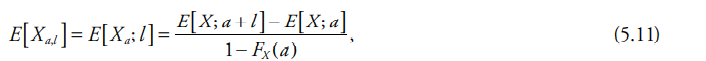
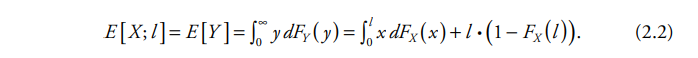
Comments
Hi,
The choice of words is unfortunately confusing but the good news is you are very close. You should basically ignore most of the words to focus on "the layer between 1,000 and 3,000" and think of this as an excess layer from a to a + L. So we're only paying out on claims in excess of 1,000 and the maximum payout is 3,000.
Then we can apply the approach you used in your scenario 1 but with the layer width being 2,000 instead of 3,000. Once you calculate E[X;3000] instead of E[X;4000] you'll arrive at 864.66 → 865.
I see, so a+L is the upper limit then, rather than L? Seems like kind of strange notation, but I thin I get it now, thanks!