Distributions - Table M and Insurance Charges (Easy)

ecasp12ecasp12
in Fisher.AggExcess

Can you show how you derived the dF(y) distribution in the Table M and Insurance Charges (Easy) problem set?

Fisher Agg Excess Uniform Equations.png

Even after reading the source material, I can't understand how to go from a uniform distribution for the actual losses to this distribution for Y = A/E.

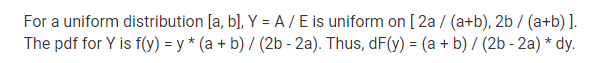
Comments

  • adminadmin

    The key to this is to use the relationship shown in the PDF for calculating the insurance savings from first principles in the Fisher.AggExcess wiki. Namely, if Y = pX+b then f_Y(y) = 1/ |p|*f_X( (y-q)/p).

    Here X is uniform on [a,b] so E = (a+b)/2. Then p = 1/E = 2/(a+b) and q=0

    So f_Y(y) = (a+b)/2 * f_X( y * (a+b)/2)

    But f_X is a constant as X is a uniform distribution.

    So f_Y(y) = (a+b)/2 * 1/(b-a) = (a+b) / (2b - 2a)

    Now integrate this from a/E to y to get F(y).

    F(y) = (a+b)/(2b-2a)*y - a/(b-a)

    But we want dF(y) so differentiating yields dF(y) = (a+b)/(2b-2a)*dy

    We've clarified the exposition in the web template to show the p.d.f and the c.d.f steps in the Cheat! section.

    Hope this helps

Sign In or Register to comment.