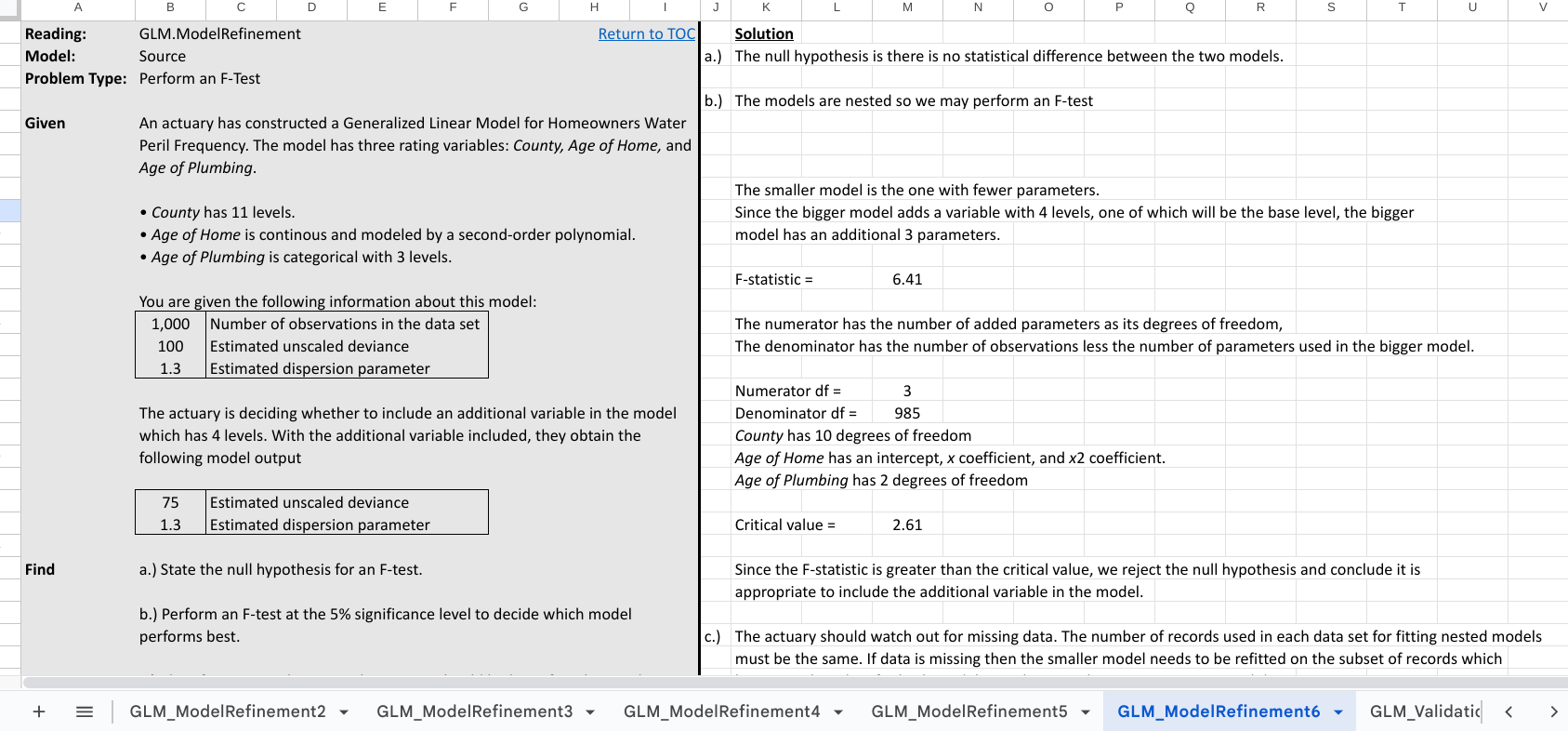
GLM_ModelRefinement6 degrees of freedom
in GLM.Basics
Should the denominator df here subtract 3 additional df in order to incorporate the new variable with 4 levels, since that will be in the "bigger" model?
Also, in the previous problem (GLM_ModelRefinement5), we said that a 2nd order polynomial added 2 parameters, but here we're saying that a 2nd order polynomial adds 3 degrees of freedom. Maybe this is a subtle distinction between parameters and degrees of freedom that I'm not picking up on. However, the wiki seems to make a direct connection between them.
Thanks in advance!

Comments
For GLM_ModelRefinement6, you are correct. The denominator has n - the number of parameters in the bigger model so we need to subtract an additional 3. I've updated the solution file online.
For GLM_ModelRefinement5, this is nuanced. It's implicit the small model already contains an intercept. When we add a second order polynomial ax^2 + bx + c we alter the existing intercept by c. So we only gain two new parameters, a and b, rather than 3.
In GLM_ModelRefinement6 we are explicitly counting all parameters as we're given an exhaustive list of the variables. The intercept is a parameter and is counted either as the base level for a categorical or the intercept for the second-order polynomial. The key thing is you want to avoid double counting the intercept (or worse) when calculating the number of parameters.
That makes sense. Thanks!